LeetCodeって?
LeetCodeとは、アルゴリズムやデータ構造を実践を通して学べる海外のプログラミング学習サイトです。
2022年12月現在2,000問を超える問題が登録されています。
各問題では、特定の入力をしたときに特定の返り値を出力する関数を作成することを求められます。
正誤判定は自動で行われます。
使用できる言語は、C++、C#、JAVA、Python3、Go、JSなど19言語が用意されています。
私はPython3で解いています。

Pythonではじめるアルゴリズム入門 伝統的なアルゴリズムで学ぶ定石と計算量 [ 増井 敏克 ]
問題
タイトル:15. 3Sum
難易度:Medium
内容:
整数が入ったリスト nums が与えられる。nums の足すと0になる3つの値の組み合わせを全て列挙する。
ない場合は空のリストを返す。
例:
nums = [-1,0,1,2,-1,-4] 返り値: [[-1,-1,2],[-1,0,1]]
nums = [0,1,1] 返り値: []
nums = [0,0,0] 返り値: [[0,0,0]]
なお、組み合わせの順番は問わない。
[[-1,-1,2], [-1,0,1]] → [[0,1,-1], [2,-1,-1]]でもOK
回答
総当たりでやる方法と、場合分けして考えるやり方を考えてみます。
総当たり
タイムオーバーになるのを承知で作ってます。
説明は面倒なので飛ばしますが、すべての組み合わせを試して、重複する回答を除いています。
#総当たり
class Solution:
def threeSum(self, nums: list[int]) -> list[list[int]]:
ans = []
nums_len = len(nums)
for i in range(nums_len):
for j in range(nums_len - i - 1):
for l in range(nums_len - i - j - 2):
if nums[i] + nums[j + i + 1] + nums[l + i + j + 2] == 0:
ans.append([nums[i], nums[j + i + 1], nums[l + i + j + 2]])
rm = []
for i in range(len(ans)):
for j in range(len(ans) - i - 1):
if sorted(ans[i]) == sorted(ans[j + i + 1]):
rm.append(ans[j + i + 1])
break
for i in range(len(rm)):
ans.remove(rm[i])
return ans結果

案の定時間かかりすぎで怒られました。
場合分け
3つの数値を x, y, z として、以下3つの場合に分けてそれぞれを見つけることを考えてみます。
コードが少し冗長になりますが割と理解しやすい解法じゃないかと思います。
1.x + x + x = 0
3つの数値が同じ場合です。
これは[0,0,0]しかありません。
2.x + y + y = 0
2つのみが同じ値の場合です。
[-2, 1, 1] などです。
x = -2y となるので、x は偶数、x, y どちらかが負の値になります。
3.x + y + z = 0
すべて別の値の場合です。
[-3, 1, 2] などです。
1つまたは2つの値が負の値になります。
実装
何はともあれソートしましょう。ついでに返り値を初期化しておきます。
nums_sorted = sorted(nums) # ソート
ans = []1,2,3では同じ値が何回出現するかを考慮しています。なので、 nums_sorted 内で同じ値が何回出現するかをカウントして保持しておきます。
保持には辞書型を使用ます。また辞書型はインデックスを持てないので、インデックス用としてリスト型の変数も定義しておきます。

nums_dict = {} # 辞書型
nums_unique = [] # リスト型、辞書のインデックス
辞書とインデックスに値を詰めていきます。
初めて出てきた値であれば辞書とインデックスに詰め、既出であれば辞書のカウントをインクリメントします。
for i in nums_sorted:
if i not in nums_dict: # 初出の値であれば
nums_dict[i] = 1 # カウント1として辞書に登録
nums_unique.append(i) # インデックスに登録
else: # 既出の値であれば
nums_dict[i] += 1 # 辞書カウントを1インクリメント1.x + x + x = 0 の場合
[0, 0, 0]の組み合わせしかありませんから、辞書に0があるか、カウントが3以上かを確認し該当すれば[0, 0, 0]を回答に追加します。
if 0 in nums_dict:
if nums_dict[0] > 2:
ans.append([0,0,0])2.x + y + y = 0 の場合
x に該当する値をインデックスから探します。x は偶数かつ 0 でない(0 の場合1.x + x + x = 0 と同じになってしまうので)値です。
次に y は x を2で割って正負を逆にしたものです。辞書に y があるか、カウントが2以上であるかを確認し、該当すれば[x, y, y]を回答に追加します。
for x in nums_unique:
if x % 2 != 0 or x == 0: # 2が奇数または0であれば
continue # 次へ
y = -x // 2
if y in nums_dict: # y が辞書に登録されており
if nums_dict[y] > 1: # カウントが2以上であれば
ans.append([x,y,y]) # 回答に[x, y, y]を追加3.x + y + z = 0
3つ全て別の値なのでインデックスの nums_unique のみを見ていきます。
なお、x, y, z のどれか1つか2つは必ず負の値になるので、x は必ず負、zは必ず正とします。
x をリスト中の一番小さい値とし、y と z で2 pointerを行います。
2 pointerについては以下の記事で解説しています。
まず x は一番小さいの値、y はその次、z は一番大きい値とします。
x + y + z < 0 なので y を1つ右に移動します。
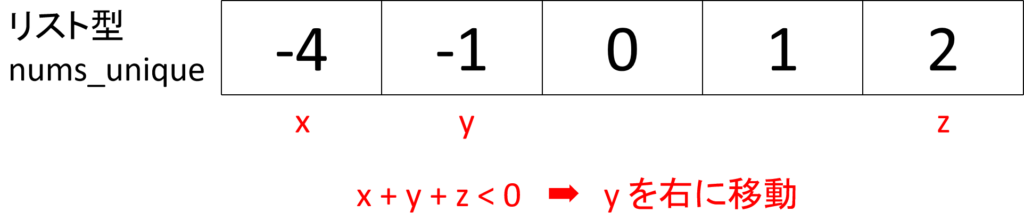
これをしていくと以下の状態になり、x = -4 では和が0になる組み合わせは見つからないことが分かります。
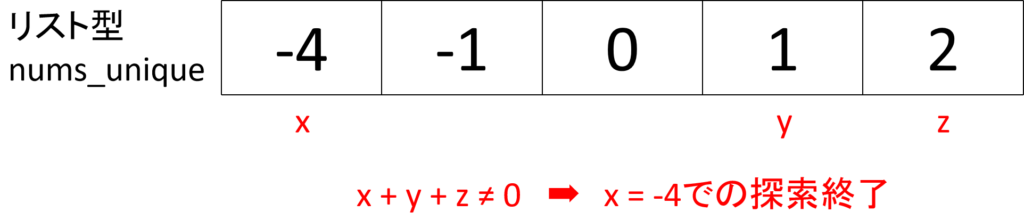
次は、x = -1 とします。
今度は x + y + z > 0 となるので、z を1つ左に移動します。

すると x + y + z = 0 が見つかりました。
返り値に [x, y, z] を追加します。
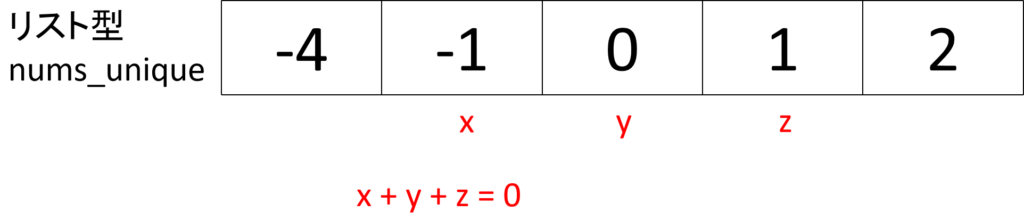
以上の理論を実装します。
for i, x in enumerate(nums_unique):
if x >= 0 or i > len(nums_unique) - 2: # x > 0 に限定、またy, zがあるので i = len(nums_unique) - 2 まで
break
L = R = 0 # 2pointer
while(i + L + 1 < len(nums_unique) - R - 1): # y < z である限り
y = nums_unique[i + L + 1]
z = nums_unique[len(nums_unique) - R - 1]
if z < 0 : break # z > 0に限定
if x + y + z == 0 : ans.append([x, y, z]) # 和が0なら[x, y, z]を返り値に追加
if x + y + z <= 0 : L += 1 # 0以下ならLをインクリメント
if x + y + z >= 0 : R += 1 # 0以下ならRをインクリメントコード
コード全文です。
class Solution:
def threeSum(self, nums: list[int]) -> list[list[int]]:
nums_sorted = sorted(nums)
ans = []
nums_dict = {}
nums_unique = []
for i in nums_sorted:
if i not in nums_dict:
nums_dict[i] = 1
nums_unique.append(i)
else:
nums_dict[i] += 1
if 0 in nums_dict:
if nums_dict[0] > 2:
ans.append([0,0,0])
for x in nums_unique:
if x % 2 != 0 or x == 0:
continue
y = -x // 2
if y in nums_dict:
if nums_dict[y] > 1:
ans.append([x,y,y])
for i, x in enumerate(nums_unique):
if x >= 0 or i > len(nums_unique) - 2:
break
L = R = 0
while(i + L + 1 < len(nums_unique) - R - 1):
y = nums_unique[i + L + 1]
z = nums_unique[len(nums_unique) - R - 1]
if z < 0 : break
if x + y + z == 0 : ans.append([x, y, z])
if x + y + z <= 0 : L += 1
if x + y + z >= 0 : R += 1
return ans計算量は x + y + z = 0 のところでO(N2)です。
コードはgithubにも保管しています。
結果
コードは冗長ですがそこまで悪くない結果だと思います。
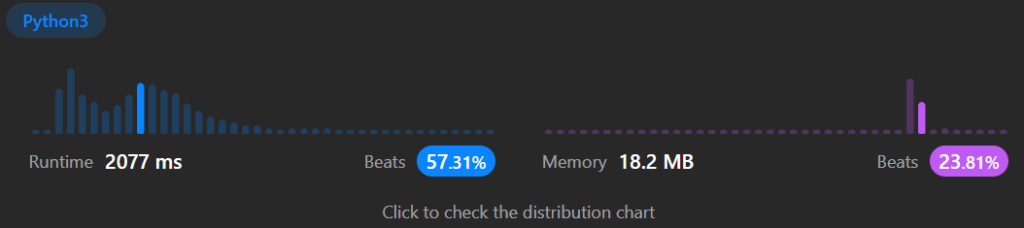
基本的に問題を解いた後に Solutions の回答例を見ているのですが、こんなやり方を見つけました。
set() を使うと重複する数値を消すことができるんですね。知りませんでした。
まだまだ勉強がたりない。。




コメント