LeetCodeって？
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
LeetCodeとは、アルゴリズムやデータ構造を実践を通して学べる海外のプログラミング学習サイトです。
2022年12月現在2,000問を超える問題が登録されています。
各問題では、特定の入力をしたときに特定の返り値を出力する関数を作成することを求められます。
正誤判定は自動で行われます。
使用できる言語は、C++、C#、JAVA、Python3、Go、JSなど19言語が用意されています。
私はPython3で解いています。
問題
Longest Palindromic Substring - LeetCode
Can you solve this real interview question? Longest Palindromic Substring - Given a string s, return the longest palindromic substring in s.
Example 1:
In...
leetcode.com
タイトル：5. Longest Palindromic Substring
難易度：Medium
内容：
文字列 s が与えられる。s に含まれる部分文字列のうち最も長い回文を返す。
例：
s = "babad" 返り値: "bab" または "aba"
Input: s = "cbbd" Output: "bb"
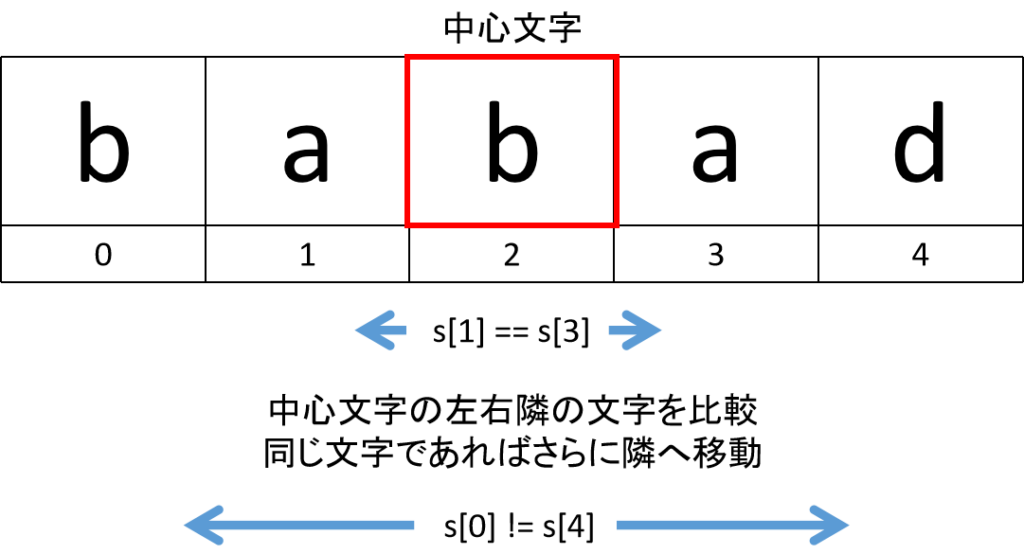
奇数文字列の回文の場合と、偶数文字列の回文の場合で中央の文字数が変わることに注意が必要です。
回答
奇数文字列の回文を検出する処理と、偶数文字列の回文を検出する処理を行います。
奇数の場合、中心となる1文字を決め、その両隣の文字が同じかどうか確認します。
同じであればさらにその隣、というようにしていき最長の回文を探します。
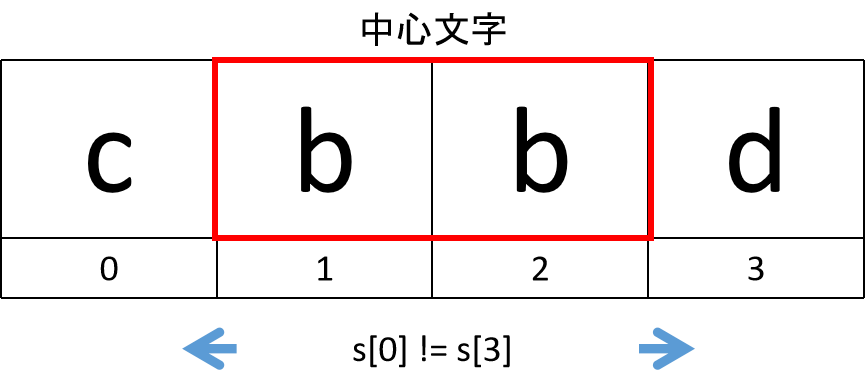
偶数の場合も中心文字が2文字になるだけでやり方は同じです。
コードを以下に示します。
コード
class Solution:
def longestPalindrome(self, s: str) -> str:
maxPalindrome = s[0]
#奇数回文
for i in range(len(s)):
# 見つかっている回文の長さに応じて処理をスキップ
# 例："abcba"の場合、4,5文字目を探索する必要はない
if i > len(s) - (len(maxPalindrome) - 1) // 2:
break
L = i - 1 # 中心文字の左側
R = i + 1 # 中心文字の右側
# 文字列の範囲を出ない限り
while L > -1 and R < len(s):
# 左と右の文字が同じであれば
if s[L] == s[R]:
# これまで見つかった回文より長かったら
if R - L + 1 > len(maxPalindrome):
maxPalindrome = s[L:R+1] # 最長の回文とする
else: break
L -= 1 # 左側更新
R += 1 # 右側更新
# 偶数回文
for i in range(len(s)):
if i > len(s) - len(maxPalindrome) // 2:
break
L = i #左側の中心文字
R = i + 1 #右側の中心文字
while L > -1 and R < len(s):
if s[L] == s[R]:
if R - L + 1 > len(maxPalindrome):
maxPalindrome = s[L:R+1]
else: break
L -= 1
R += 1
return maxPalindrome二重ループとなるので計算量はO(N2)です。
奇数文字列回文と偶数文字列回文を同じforループの中にまとめてもよかったのですが、わかりにくくなりそうなので分けてます。
同じforループに入れる場合は、イテレーション数を2倍にし、Lの初期化の際に
L = i – 1 と L = i が交互に来るようにすればできると思います。
コードはgithubにも保管しています。
https://github.com/BB-engineer/LeetCode
結果
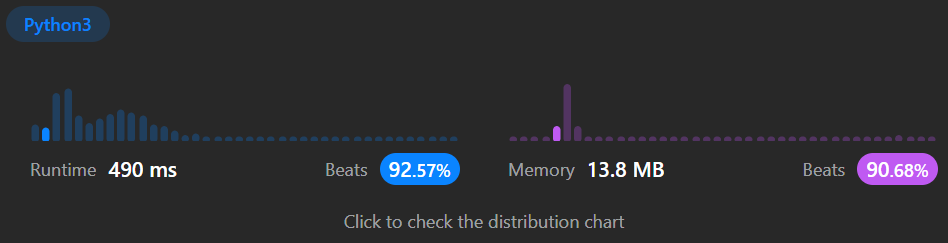
O(N2)の割には速い結果がでました。
コメント